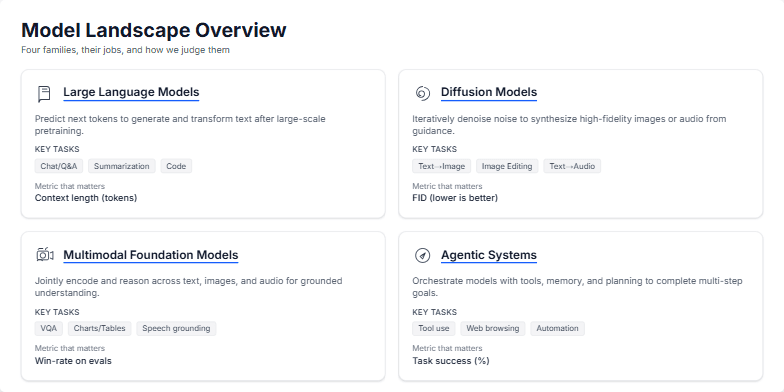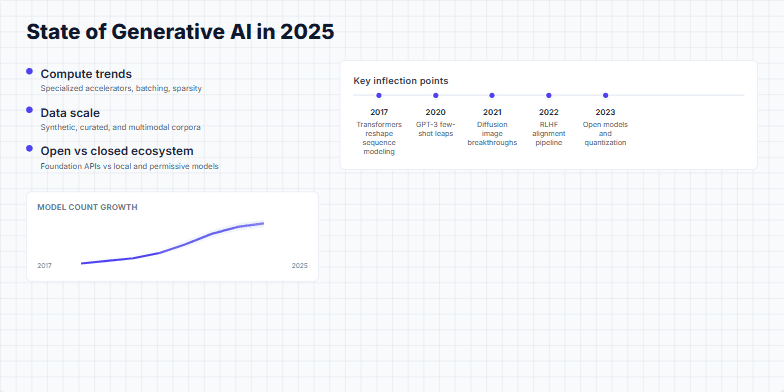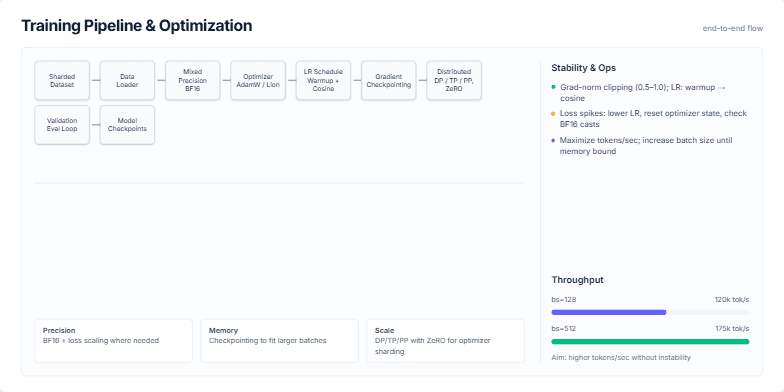
Visualizing a Modern Deep Learning Training Pipeline and Key Optimization Strategies for Stability and Throughput.
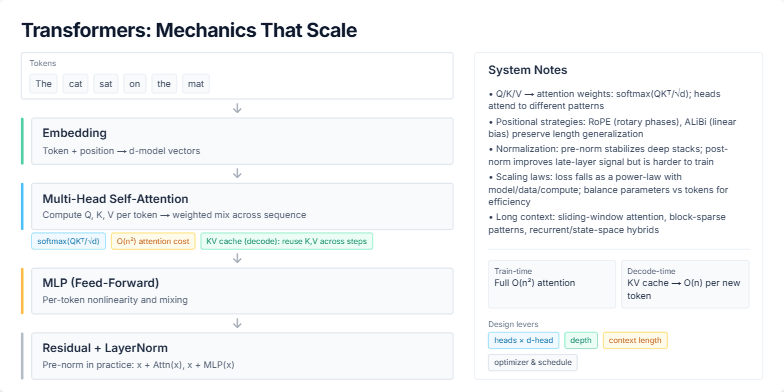
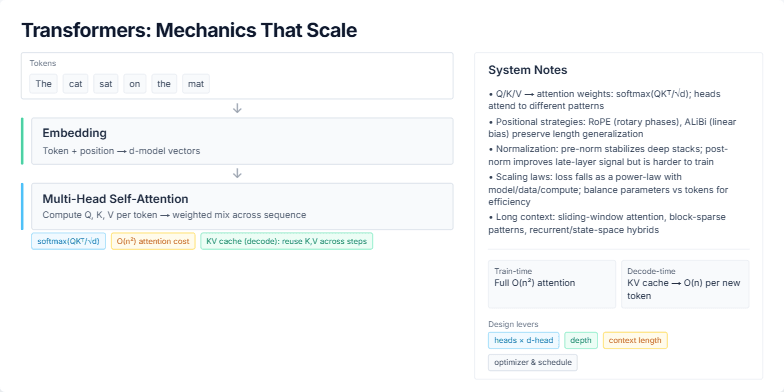
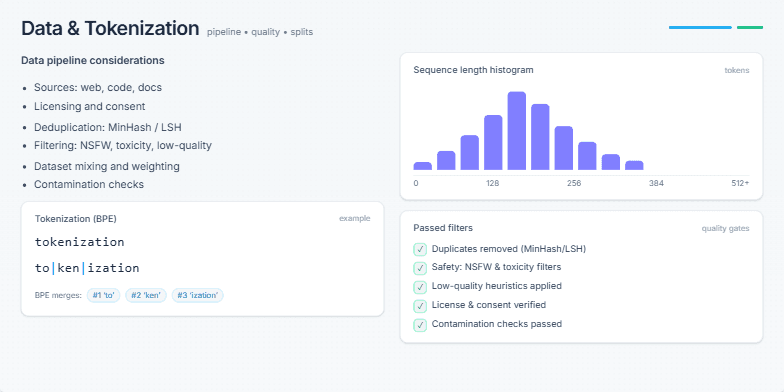
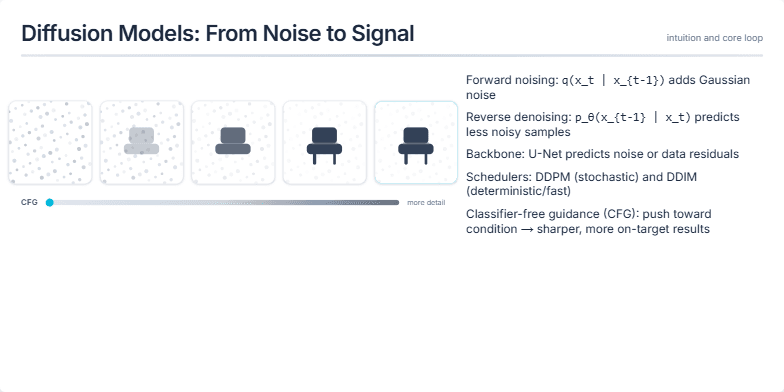
Create a slide that visually breaks down a standard end-to-end training pipeline for a large language model (LLM). It should start from the dataset and go all the way to model checkpoints. For each stage, like data loading, mixed precision, and distributed training, show the key technologies or concepts (e.g., BF16, AdamW, ZeRO). The slide should also include a sidebar with practical tips on ensuring training stability (like handling loss spikes) and a section on optimizing for throughput, showing how batch size affects tokens/second. The overall aesthetic should be clean, technical, and professional.